Explainer: What are logarithms and exponents?
Math offers a way to track and compare data that vary dramatically in size

Logarithms are mathematical relationships used to compare things that can vary dramatically in scale.
Benjaminec/iStock/Getty Images Plus
Share this:
- Share via email (Opens in new window) Email
- Click to share on Facebook (Opens in new window) Facebook
- Click to share on X (Opens in new window) X
- Click to share on Pinterest (Opens in new window) Pinterest
- Click to share on Reddit (Opens in new window) Reddit
- Share to Google Classroom (Opens in new window) Google Classroom
- Click to print (Opens in new window) Print
When COVID-19 hit the United States, the numbers just seemed to explode. First, there were only one or two cases. Then there were 10. Then 100. Then thousands and then hundreds of thousands. Increases like this are hard to understand. But exponents and logarithms can help make sense of those dramatic increases.
Scientists often describe trends that increase very dramatically as being exponential. It means that things don’t increase (or decrease) at a steady pace or rate. It means the rate changes at some increasing pace.
An example is the decibel scale, which measures sound pressure level. It is one way to describe the strength of a sound wave. It’s not quite the same thing as loudness, in terms of human hearing, but it’s close. For every 10 decibel increase, the sound pressure increases 10 times. So a 20 decibel sound has not twice the sound pressure of 10 decibels, but 10 times that level. And the sound pressure level of a 50 decibel noise is 10,000 times greater than a 10-decibel whisper (because you’ve multiplied 10 x 10 x 10 x 10).
An exponent is a number that tells you how many times to multiply some base number by itself. In that example above, the base is 10. So using exponents, you could say that 50 decibels is 104 times as loud as 10 decibels. Exponents are shown as a superscript — a little number to the upper right of the base number. And that little 4 means you’re to multiply 10 times itself four times. Again, it’s 10 x 10 x 10 x 10 (or 10,000).
Logarithms are the inverse of exponents. A logarithm (or log) is the mathematical expression used to answer the question: How many times must one “base” number be multiplied by itself to get some other particular number?
For instance, how many times must a base of 10 be multiplied by itself to get 1,000? The answer is 3 (1,000 = 10 × 10 × 10). So the logarithm base 10 of 1,000 is 3. It’s written using a subscript (small number) to the lower right of the base number. So the statement would be log10(1,000) = 3.
At first, the idea of a logarithm might seem unfamiliar. But you probably already think logarithmically about numbers. You just don’t realize it.
Let’s think about how many digits a number has. The number 100 is 10 times as big as the number 10, but it only has one more digit. The number 1,000,000 is 100,000 times as big as 10, but it only has five more digits. The number of digits a number has grows logarithmically. And thinking about numbers also shows why logarithms can be useful for displaying data. Can you imagine if every time you wrote the number 1,000,000 you had to write down a million tally marks? You’d be there all week! But the “place value system” we use allows us to write down numbers in a much more efficient way.
Why describe things as logs and exponents?
Log scales can be useful because some types of human perception are logarithmic. In the case of sound, we perceive a conversation in a noisy room (60 dB) to be just a bit louder than a conversation in a quiet room (50 dB). Yet the sound pressure level of voices in the noisy room might be 10 times higher.
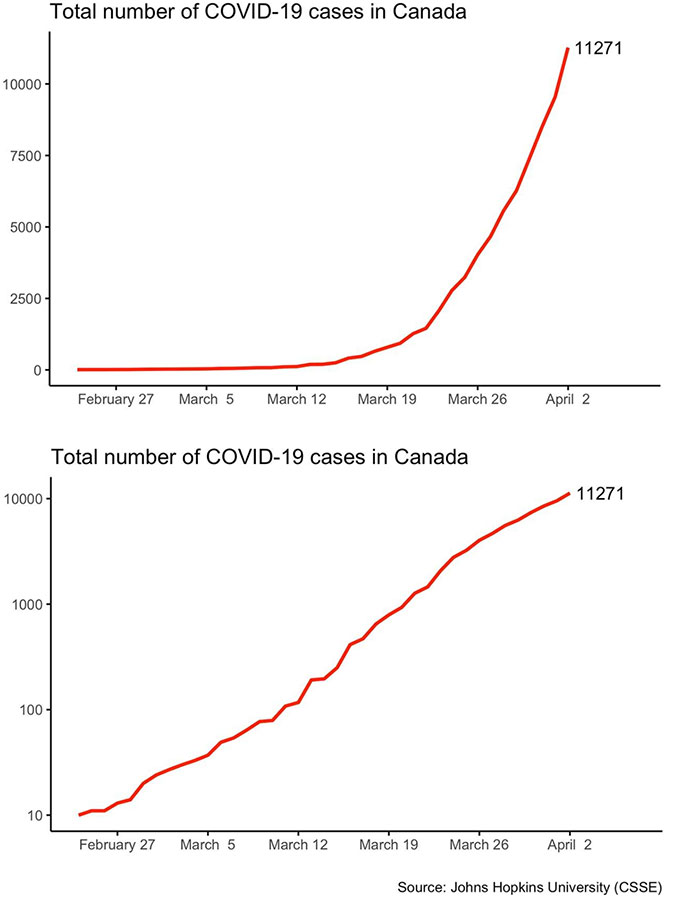
Another reason to use a log scale is that it allows scientists to show data easily. It would be hard to fit the 10 million lines on a sheet of graph paper that would be needed to plot the differences from a quiet whisper (30 decibels) to the sound of a jackhammer (100 decibels). But they’ll easily fit on a page using a scale that’s logarithmic. It’s also an easy way to see and understand big changes such as rates of growth (for a puppy, a tree or a country’s economy). Any time you see the phrase “order of magnitude,” you’re seeing a reference to a logarithm.
Logarithms have many uses in science. pH — the measure of how acidic or basic a solution is — is logarithmic. So is the Richter scale for measuring earthquake strength.
In 2020, the term logarithmic became best known to the public for its use in describing the spread of the new pandemic coronavirus (SARS-CoV-2). As long as each person who got infected spread the virus to no more than one other person, the size of the infection would stay the same or die out. But if the number was more than 1, it would increase “exponentially” — which means that a logarithmic scale could be useful to graph it.
Basic bases
The base number of a logarithm can be almost any number. But there are three bases which are especially common for science and other uses.
- Binary logarithm: This is a logarithm where the base number is two. Binary logarithms are the basis for the binary numeral system, which allows people to count using only the numbers zero and one. Binary logarithms are important in computer science. They’re also used in music theory. A binary logarithm describes the number of octaves between two musical notes.
- Natural logarithm: A so-called “natural” logarithm — written ln — is used in many areas of math and science. Here the base number is an irrational number referred to as e, or Euler’s number. (The mathematician Leonhard Euler did not intend to name it after himself. He was writing a math paper using letters to represent numbers and happened to use e for this number.) That e is about 2.72 (though you can never write it down completely in decimals). The number e has some very special mathematical properties that make it useful in many areas of math and science, including chemistry, economics (the study of wealth) and statistics. Researchers also have used the natural logarithm to define the curve that describes how a dog’s age relates to a human one.
- Common logarithm: This is a logarithm where the base number is 10. This is the logarithm used in measurements for sound, pH, electricity and light.