How to Slice a Cake Fairly

Sharing can be hard. Every kid knows that, and mathematicians do, too. So mathematicians have spent a lot of time thinking about how to make sharing easier.

Mathematicians are particularly fond of sharing birthday cake. Not just any birthday cake, but one with lots of icing and various decorations, with nuts here and coconut there. Then they ask, if two people like different parts of the cake better, how can they divide the cake into two pieces so that they’re both satisfied with the piece that they each get?

You and your friend want to divide a cake into two pieces in such a way that each of you is happy with the piece that you get. How would you do it?

There’s an old solution known as “I cut, you choose.” You start by cutting the cake into two pieces that you like equally well. Then your friend picks the one that she prefers.

The two pieces don’t have to be the same size. If you particularly like nuts, for example, you might make the piece with fewer nuts bigger, so that you’d be happy no matter which piece your friend chose. You’d end up with either a smaller piece with lots of nuts or a larger piece with fewer nuts.

But Steven Brams of New York University doesn’t think that’s fair. When you’re done, you get a piece that you might think is worth half the value of the cake. But your friend might think that she got much more than half the value of the cake.

For example, suppose that your friend really likes coconut, and the bigger, less nutty piece has lots of coconut. Then she’ll think that she’s gotten a really great deal. She got not only more cake but also the best part!

Brams says that a division should be considered fair only if two people think they both got pieces of the same value. He’s worked out a new procedure for cake-cutting that makes this happen.

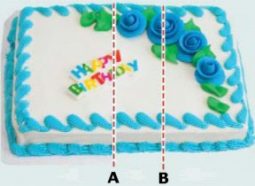In dividing this cake, A marks the cut where you think the two pieces have equal value. B shows the division where your friend thinks the two pieces are equal. By a new method, you’d get the leftmost piece and your friend would get the rightmost piece, an

E. Roell

Here’s how it works. You and your friend would each tell your mom where you would divide the cake into two pieces. If the two of you happen to pick the same spot, she’d simply divide the cake at that spot. Both of you would be equally happy with your shares.

But suppose the two spots are different. If your spot were to the left of your friend’s spot, you’d get the piece to the left of your spot. Your friend would get the piece to the right of her spot. And there’d be a piece left over in the middle. Your mom would then split the middle section between you and your friend.

That way, you each get a piece that you value equally—plus a bonus!

It’s a neat idea, but is such a procedure practical? Would you use it?

“I don’t know if anyone other than me has actually brought a cake in and tried to divide it,” says James Tanton, a mathematics teacher at St. Mark’s School in Southborough Mass. Such schemes often don’t work in practice. “Human beings are too fuzzy,” he says. “They change their minds.”—J.J. Rehmeyer

Going Deeper:

Rehmeyer, Julie J. 2006. A fair slice: New method makes for equitable eating. Science News 170(Dec. 16):390. Available at http://www.sciencenews.org/articles/20061216/fob7.asp .

Peterson, I. 1999. Fair shares. Muse 3(May/June):28. Available at www.sciencenewsforkids.org/pages/puzzlezone/
muse/muse0599.asp.

______. 1996. Formulas for fairness. Science News 149(May 4):284-285. Available at http://www.sciencenews.org/pages/sn_arch/5_4_96/bob1.htm .