Cookie Science 10: Finding the cookie difference
Statistics will help me determine if people liked one cookie more than the others
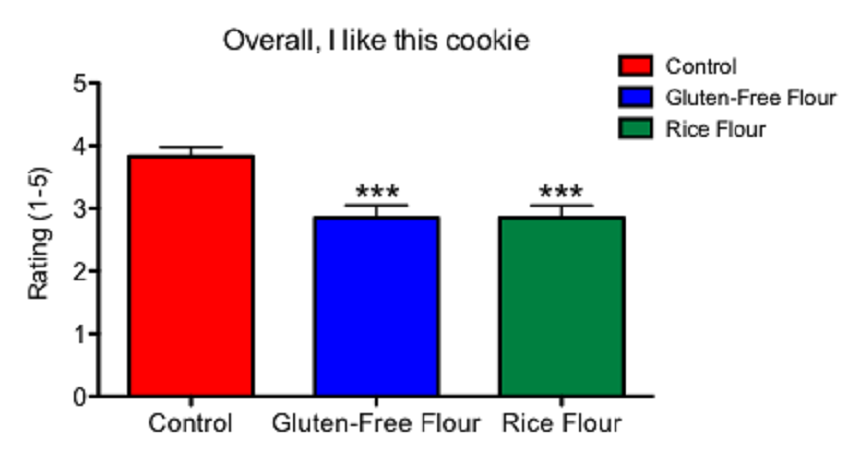
This graph shows the results of my first experiment and how people ranked three different types of cookies. It is based on a statistical test known as ANOVA.
B. Brookshire/SSP
Share this:
- Share via email (Opens in new window) Email
- Click to share on Facebook (Opens in new window) Facebook
- Click to share on X (Opens in new window) X
- Click to share on Pinterest (Opens in new window) Pinterest
- Click to share on Reddit (Opens in new window) Reddit
- Share to Google Classroom (Opens in new window) Google Classroom
- Click to print (Opens in new window) Print
This article is one of a series of Experiments meant to teach students about how science is done, from generating a hypothesis to designing an experiment to analyzing the results with statistics. You can repeat the steps here and compare your results — or use this as inspiration to design your own experiment.
People have eaten my control and gluten-free chocolate-chip cookies. They ranked them according to statements such as “Overall, I like this cookie.” Now I need math to tell me if the rankings are really different — despite what the numbers seem to show. I can use some simple statistics to tell me how big the difference is between my cookies. Once I know the difference, I can make conclusions about my data.
It may seem like a lot of math. But it’s not too bad when it’s broken down into small chunks. This math is worth it. It means we can judge when a difference between groups is believable. And that is very important for all types of science.
In the last blog, I noted that we need to calculate an analysis of variance, or ANOVA. Researchers turn to this test when they need to compare data collected on two or more groups of variables (such as the different cookie recipes in my experiment). The test doesn’t just use the mean — or central value — of the data. It also compares variance, or how much the data in each list of numbers spreads out within that list. An ANOVA, compares the spread of numbers within each group to the spread of means between the groups.
I can calculate an ANOVA with a pencil and paper or with a calculator, but you don’t have to. There are free programs on the Internet that can run the math for us. Some are so easy we can just plug in the original numbers and the program will do the rest. If you choose to use one of these automatic programs, they will display your results a certain way. If you understand how the ANOVA works, you will be able to figure out what the numbers the program gives you mean in terms of your tests.
I am using a program called GraphPad. This software is not free, but I like it because I can use it both to run my statistics and to make nice looking graphs of my data. The program requires me to enter the mean, the standard error of the mean and the number of test subjects (cookie tasters) per group. I already have my mean and standard error of the mean from previous posts.
The program will now use the comparisons to come up with a p value. This number represents the probability of seeing a difference in cookie rankings that is as large or larger than the difference I observed — if there was no difference in the cookies due to the flour. Scientists generally accept a p value of less than five percent (written 0.05) as statistically significant — or unlikely to be due to chance. If I run my analysis of variance and get a p value of 0.7, any differences that I see are likely to be just the result of chance, and not because of my flour.
Running a statistical test like an analysis of variance is always a nail-biting moment. It will tend to point to whether our testing results discovered something new.
| Table Analyzed | Overall, I like this cookie |
| One-way analysis of variance (ANOVA) | Yes |
| P value | 0.0001 |
| P value summary | *** |
| Are means signif. different? (P < 0.05) | Yes |
| Number of groups | 3 |
| F | 9.753 |
| R square | 0.1398 |
Above you can see a table summarizing the results of my analysis of variance. You can see in red that in my study, the difference is statistically significant. That suggests the rankings between my cookies are truly different. My p value is 0.0001 or 0.1 percent. So there is a 99.9 percent chance that I would not see a difference as big as or bigger than the one I observed unless the gluten-free flours were responsible.
The analysis of variance can tell me that there is an overall difference between my control and gluten-free data sets. But it can’t tell me whether the specific difference between the rice flour and the control is statistically significant.
For that, I need a post-hoc test. Post-hoc is Latin for “after this”. In a post-hoc test, scientists look at the data after it has been collected to find other differences they may not have predicted. And yes, this means we’ll have to do a bit more math.
This test will let me look for differences between each pair of cookies. There are many different post-hoc tests to choose from. I use one called the Tukey’s range test. It compares all possible pairs of means — such as data on the control cookies versus data for cookies made from a mix of gluten-free flours. Each combo tested will help show whether any two means are significantly different from each other.
Many programs — including some free online programs — can do this test. My Tukey’s test shows that the differences are statistically significant between my control cookie and one made using the mix of gluten-free flours (p = 0.001). It finds a similar difference between the control cookie and one made from the rice flour (p = 0.001). But it turned up no difference between the two types of gluten-free cookies.
Once I have all the data analyzed, I can put them into graphs. Graphs offer one way to see at a glance any differences between sets of data, and to show which differences are statistically significant.
I am going to put my data into a graph with three columns side by side. The control cookie will be on the left, and the two gluten-free varieties will be in columns to the right. I can display the results of my Tukey’s test as signs above each column using asterisks. Scientists typically identify statistical significance by placing these tiny star-shaped symbols above the columns in a graph (as you can see at the top of this post). One asterisk means a p value of less than 0.05 compared to control; two asterisks mean the p value is less than 0.01; three asterisks mean a p value of less than 0.001. As you can see above, my p value is 0.001. I get to use three stars in my graph. Yay!
The graph I came up with is pictured at the top of this post. On the x axis — which is the horizontal line at the bottom of the graph — you can see the three cookie groups: control (wheat flour), mix of gluten-free flours and rice flour.
On the y axis — which is the vertical line running up the left side of the graph — you can see the mean rating that people gave to the phrase: “Overall, I like this cookie.” The height of each bar on the Y axis represents the mean numerical score that people gave each cookie. The “T” above each bar represents the standard error of the mean — the probability of how much the data might spread if I were to sample an entire population. The probability is based on the people that actually tasted my cookies. So if I were to feed cookies to everyone in the world, this “T” represents what we predict that data set might look like.
I display the standard error in the graph so that anyone reading my graph will be able to see how much each cookie ranking is predicted to vary. I have the asterisks above the gluten-free flour and the rice flour bars. The asterisks indicate that the rankings for those cookies are significantly different from the ranking given the control cookie.
I now know that the differences between my cookies are statistically significant. I now can interpret what the differences mean. Still, because I cannot sample everyone in the world, I must be cautious about my conclusions. I can say only that in this experiment, the subjects who sampled my cookies did not like the gluten-free flour and rice flour cookies as much as my standard chocolate-chip cookie.
My original hypothesis predicted that substituting gluten-free flour alone would not make a cookie that is as good as my original recipe. If this hypothesis were false, my data would have shown no differences between cookie rankings. Instead, I found that my participants ranked the gluten-free and rice flour cookies very differently — in this case, worse.
I cannot say that my hypothesis is true, because there is always some possibility, however small, that my results are due to chance. But I can say that this experiment strongly supports my hypothesis.
Follow Eureka! Lab on Twitter
Power Words
ANOVA The acronym for analysis of variance, a statistical test to probe for differences between more than two test conditions.
average (in science) A word for the arithmetic mean, or the sum of a group of numbers divided by the size of the group. It can also refer to the number in the middle of a group of numbers or the number that appears most often in a data set.
axis The line about which something rotates. On a wheel, the axis would go straight through the center and stick out on either side. (in mathematics) An axis is a line to the side or bottom of a graph; it is labeled to explain the graph’s meaning and units of measurement.
control A part of an experiment where nothing changes. The control is essential to scientific experiments. It shows that any new effect must be due to only the part of the test that a researcher has altered. For example, if scientists were testing different types of fertilizer in a garden, they would want one section of to remain unfertilized, as the control. Its area would show how plants in this garden grow under normal conditions. And that give scientists something against which they can compare their experimental data.
gluten A pair of proteins — gliadin and glutenin — joined together and found in wheat, rye, spelt and barley. The bound proteins give bread, cake and cookie doughs their elasticity and chewiness. Some people may not be able to comfortably tolerate gluten, however, because of a gluten allergy or celiac disease.
hypothesis A proposed explanation for a phenomenon. In science, a hypothesis is an idea that hasn’t yet been rigorously tested. Once a hypothesis has been extensively tested and is generally accepted to be the accurate explanation for an observation, it becomes a scientific theory.
Likert scale One of the most commonly used ways for ranking opinions or statements in surveys involving people. A issues a series of statements, such as “I like X,” “the test was easy,” or “it was too loud.” Participants then rate how well they agree by choosing from a range options that might range from “strongly agree” to “strongly disagree.”
mean One of several measures of the “average size” of a data set. Most commonly used is the arithmetic mean, obtained by adding the data and dividing by the number of data points.
post-hoc test (In statistics) An analysis of a data set after an experiment has concluded. A post-hoc test looks for patterns that were not necessarily predicted when the scientists began the experiment.
statistics The practice or science of collecting and analyzing numerical data in large quantities and interpreting their meaning. Much of this work involves reducing errors that might be attributable to random variation. A professional who works in this field is called a statistician.
statistical analysis Mathematical processes that allow a scientists to make conclusions from a set of data.
statistical significance In research, a result is significant (from a statistical point of view) if the likelihood that an observed difference between two or more conditions would not be due to chance. Obtaining a result that is statistically significant means there is a very high likelihood that any difference that is measured was not the result of random accidents.
standard deviation (in statistics) The amount that each set of data varies from the mean.
standard error of the mean (in statistics)The probable distribution of numbers based on a random sample.
Tukey’s range test (in statistics) A test that compares all possible pairs of means to determine if they are significantly different from each other.
variable (in mathematics) A letter used in a mathematical expression that may take on more than one different value. (in experiments) A factor that can be changed, especially one allowed to change in a scientific experiment. For instance, when measuring how much insecticide it might take to kill a fly, researchers might change the dose or the age at which the insect is exposed. Both the dose and age would be variables in this experiment.
variance (in mathematics) The average of the squared distances of each number from the mean of the number list.
x axis (in mathematics) The horizontal line at the bottom of a graph, which can be labeled to give information about what the graph represents.
y axis (in mathematics) The vertical line to the left or right of a graph, which can be labeled to give information about what the graph represents.