Cookie Science 11: That’s the way the cookie crumbles

This article is one of a series of Experiments meant to teach students about how science is done, from generating a hypothesis to designing an experiment to analyzing the results with statistics. You can repeat the steps here and compare your results — or use this as inspiration to design your own experiment. 

I’ve baked a lot of cookies for science. Now it’s time to see what the data show.

So far, it’s clear that my tasters did not like the cookies made with my two gluten-free flours as much as they did the control cookies made with normal flour. When tasters were asked how much they agreed with the statement “Overall, I like this cookie,” the gluten-free ones got significantly lower scores. But while that tells me that my participants did not like the gluten-free cookies as much, it doesn’t really tell me why.  So here I explain how I figured out what might underlie their distaste.

I need to know what it is about gluten-free cookies that my tasters didn’t like. Maybe they think gluten-free cookies don’t taste as sweet. Maybe they’re too moist or too dry. I attempted to home in on my tasters’ experiences by asking them to tell me what they thought of the following statements:

1. This cookie is sweet.
2. This cookie is chewy.
3. I like this cookie’s texture.
4. This cookie is dry.
5. Overall, I like this cookie.

After reading each, my participants selected one of five options that ranged from “strongly agree” to “strongly disagree.” I turned their selections into numbers. Then I used statistics to find out if there were differences between how people ranked the control cookies and those baked from either of the gluten-free flours. To do this, I ran a test called a one-way analysis of variance, or ANOVA. Scientists use it to compare data when their testes include two or more variables. In my case, I have three variables: cookies using the control flour, rice flour (rice is gluten-free) and flour made from a mix of gluten-free sources.

An ANOVA shows me whether the differences between all the groups are statistically significant — and not, most likely, due merely to chance. I have also run a post-hoc test, which scientists use after the original data analysis to scout for other differences that might not have been predicted for the original analysis. In my case, I used what’s called the Tukey’s range test. It allows me to compare different groups of cookies within each statement. For example, it should let me know if people ranked cookies made with the “mixed-source” gluten-free flour as being drier than the also gluten-free rice-flour cookie.

I am presenting my results in graphs, so that it is easy to see any differences between sets of data. Each graph has anx axis running along the bottom, and a y axis running along the side. The x axis for each graph is labeled with the three different types of cookies I baked (the control with wheat flour and each of the two gluten-free flours). The y axis is the mean ranking that each cookie received on the Likert scales. So if the bar is tall, it received a high Likert ranking, which means that my participants “agreed” more with the statement.

You will also see a little “T” above each bar in the graph. It represents the standard error of the mean —the likelihood of how much the data for that bar might vary if I got everyone in the world to eat the cookie and rank it.

I also have asterisks above some of the bars. These asterisks indicate when my Tukey’s test turned up a statistically significant difference between either of the gluten-free cookies and my control cookie. One asterisk is used to indicate a p value — the probability that my results are due to chance — of less than 0.05 (when compared to the control cookie). Two asterisks mean the difference yielded a p value less than 0.01 and three asterisks means there is a p value of less than 0.001. A p value less than 0.05 means there is only a five percent likelihood that the results could be due to chance. p values less than that mean seeing the results I have by accidence is even less likely.

How cookies spread

We’ll start with data that I collected before people tasted my cookies. I noticed when I baked my first batch that the gluten-free flours resulted in cookies that flattened much more than the controls and became wider. This was true even though the same amount of dough went into each cookie.

From reading research papers by other scientists on gluten-free baking, I learned that gluten-free flours can produce thinner, wider cookies. So to quantify the effect in my cookies, I used a tape measure and measured 5 control cookies and 10 of each kind of gluten-free cookie before I put them in the oven, and after they came out again, making sure to write the numbers down in my lab notebook (I should have measured 10 control cookies. I was prevented because almost all of them were baked when I started measuring. I will correct this and retake control measurements in the next experiment.) I subtracted the pre-baking width from the post-baking size to get a measure of cookie spread.

(story continues below graph)

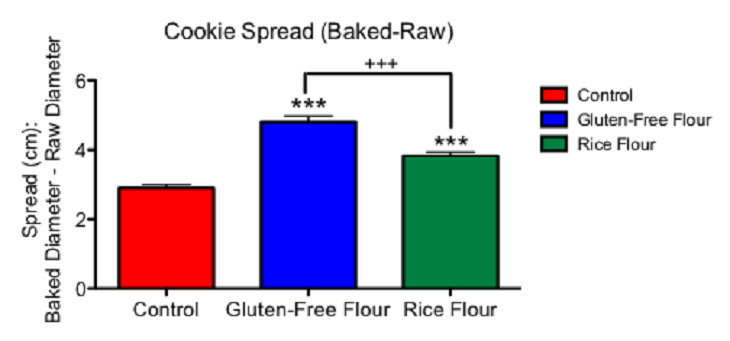
You can see my three types of cookies on the x axis. On the y axis you can see how I calculated cookie spread in centimeters. After baking, the control cookies were only about three centimeters wider than the raw cookie. But cookies made using the flour from mixed gluten-free sources were almost five centimeters wider after baking. Gluten-free rice cookies were almost four centimeters wider after baking.

I have three asterisks above the bars for the mixed gluten-free and rice gluten-free results. The p value for each is less than 0.001, which suggests the findings are reliable and quite unlikely to be due to chance. You also can see a set of plus signs linking the blue and green bars. This indicates that there is a significant difference in how much the mixed and rice gluten-free cookies had spread during baking. I used plus signs here so that those statistics will not be confused with statistics comparing gluten-free cookies to control.

Of course, a wider cookie isn’t necessarily a bad thing. What matters most is how the cookies taste. But a wider cookie will be thinner. And a thinner cookie will bake faster — so it certainly could be drier or crunchier.

How sweet they are

The first statement I posed to my readers was “This cookie is sweet.” Tasters had to rank how well they agreed with the statement. 

(story continues below graph)

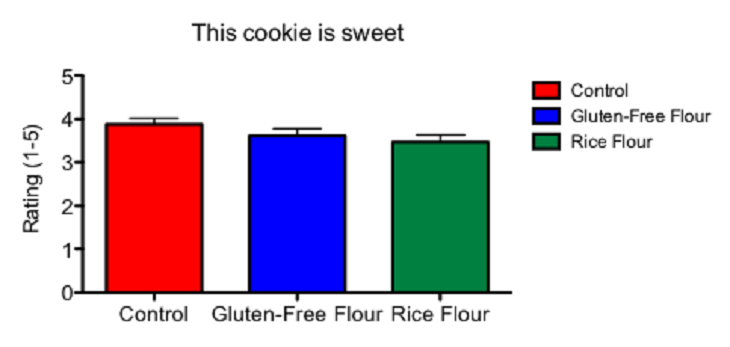
Here you can see my three types of cookies, and on the y axis, the mean ratings that my tasters gave the cookies when given the statement “This cookie is sweet.” With no asterisks in this graph, you can see that my participants generally agreed with the statement for each cookie. This means that while the gluten-free flours did affect whether people liked my cookies, it is probably not because the different flours affected the sweetness of the cookies. 

Dry cookie, chewy cookie

In a previous post, I showed that my tasters did not rate cookies made with gluten-free flours as highly as they rated control cookies. So if all of the cookies were equally sweet, what made the gluten-free less desirable?

It could be their texture. So I asked samplers to assess aspects of that.

(story continues below slideshow)

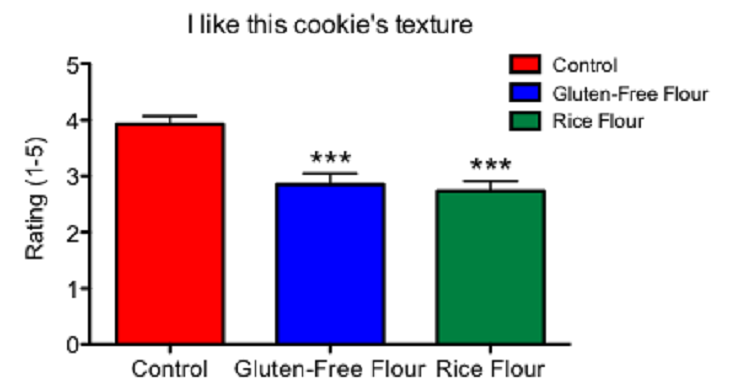
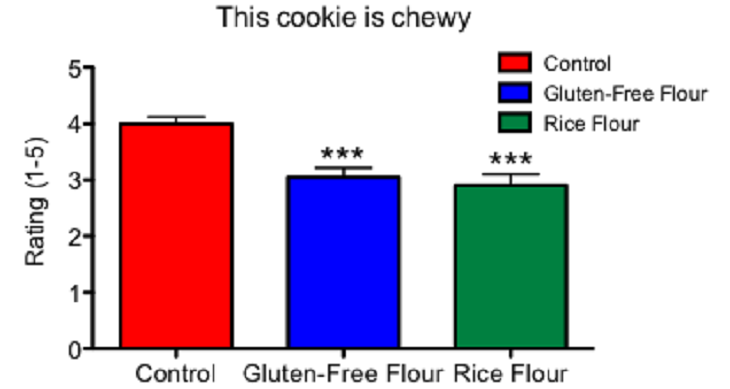
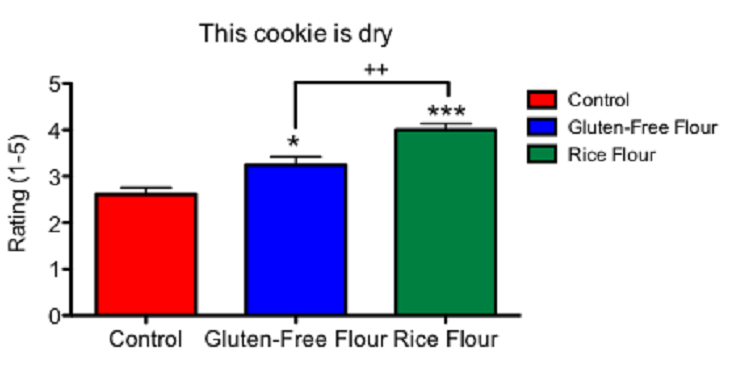
The first graph shows that the two gluten-free cookies — ones made from the gluten-free mix and the rice flour — scored lower on texture. My taste testers found both gluten-free cookies less chewy and more dry than the control cookies. In fact, they rated the rice-flour cookie driest of all.

The way the cookie crumbles

From these data, you can see that my taste testers preferred the original (control) cookie recipe. My hypothesis for this experiment was that replacing regular flour with gluten-free flour would not make a cookie as good as my control. So far, my data support that.

But I still want to make a cookie that my friend Natalie can eat. So it’s time to come up with a new hypothesis — and a new experiment — on how to bake up a tastier gluten-free cookie.

Follow Eureka! Lab on Twitter

Power Words

ANOVA     The acronym for analysis of variance, a statistical test to probe for differences between more than two test conditions.

average  (in science) A word for the arithmetic mean, or the sum of a group of numbers divided by the size of the group. It can also refer to the number in the middle of a group of numbers or the number that appears most often in a data set.

control     A part of an experiment where nothing changes. The control is essential to scientific experiments. It shows that any new effect must be due to only the part of the test that a researcher has altered. For example, if scientists were testing different types of fertilizer in a garden, they would want one section of to remain unfertilized, as the control. Its area would show how plants in this garden grow under normal conditions. And that give scientists something against which they can compare their experimental data.

gluten  A pair of proteins — gliadin and glutenin — joined together and found in wheat, rye, spelt and barley. The bound proteins give bread, cake and cookie doughs their elasticity and chewiness. Some people may not be able to comfortably tolerate gluten, however, because of a gluten allergy or celiac disease.

hypothesis  A proposed explanation for a phenomenon. In science, a hypothesis is an idea that hasn’t yet been rigorously tested. Once a hypothesis has been extensively tested and is generally accepted to be the accurate explanation for an observation, it becomes a scientific theory.

Likert scale  One of the most commonly used ways for ranking opinions or statements in surveys involving people. A issues a series of statements, such as “I like X,” “the test was easy,” or “it was too loud.” Participants then rate how well they agree by choosing from a range options that might range from “strongly agree” to “strongly disagree.”

mean  One of several measures of the “average size” of a data set. Most commonly used is the arithmetic mean, obtained by adding the data and dividing by the number of data points.

post-hoc test  (In statistics) An analysis of a data set after an experiment has concluded. A post-hoc test looks for patterns that were not necessarily predicted when the scientists began the experiment.

statistics  The practice or science of collecting and analyzing numerical data in large quantities and interpreting their meaning. Much of this work involves reducing errors that might be attributable to random variation. A professional who works in this field is called a statistician.

statistical analysis  Mathematical processes that allow a scientists to make conclusions from a set of data.

statistical significance  In research, a result is significant (from a statistical point of view) if the likelihood that an observed difference between two or more conditions would not be due to chance. Obtaining a result that is statistically significant means there is a very high likelihood that any difference that is measured was not the result of random accidents.

standard deviation (in statistics) The amount that each set of data varies from the mean.

standard error of the mean (in statistics)The probable distribution of numbers based on a random sample.

Tukey’s range test  (in statistics) A test that compares all possible pairs of means to determine if they are significantly different from each other.

variable  (in mathematics) A letter used in a mathematical expression that may take on more than one different value. (in experiments) A factor that can be changed, especially one allowed to change in a scientific experiment. For instance, when measuring how much insecticide it might take to kill a fly, researchers might change the dose or the age at which the insect is exposed. Both the dose and age would be variables in this experiment.

variance  (in mathematics) The average of the squared distances of each number from the mean of the number list.