Supreme Court shies away from test on the math of voting rights

In a democracy, voters get to pick their leaders. And every vote should have the same weight in selecting the winner. Indeed, under the U.S. Constitution, there is a general principal: One person, one vote. In some states, however, some votes may not carry the same weight.

Here’s why.

In the United States, many elected officials at the state and federal levels represent people in particular districts, or areas. In most cases, states decide the boundaries for those districts. But, sometimes, the people who draw those boundary lines may deliberately give a big advantage to one political party. This is called gerrymandering, and it’s not fair.

Moon Duchin is a mathematician at Tufts University in Medford, Mass. “Gerrymandering is basically a math problem,” she explains. “It’s asking how you can divide something up so the division has certain properties.” In this case, one group wants the boundaries of the voting districts to include more people from one political party or from a certain interest group. In this way, district voters will likely give a win to a selected party or group.

Last year, some voters in Wisconsin legally challenged what they claimed were gerrymandered districts. Another case in Maryland challenged changes to one district’s boundary lines. The cases went all the way to the Supreme Court. The high court has just handed down its decisions.

On June 18, the court ruled against the Wisconsin challengers. All nine justices found that individual voters could not challenge the whole state’s voting district map. But seven justices left open the possibility for individuals to challenge the lines of their individual districts.

On the same day, the court also ruled against the Maryland challengers. The challengers had wanted the lower court to prevent use of the old voting district map until the case was finished. But that’s a matter of discretion for the trial judge.

Both decisions essentially sidestepped the basic question: When, if ever, do districts drawn to favor one party over another violate the U.S. Constitution?

Choosing voters

Political parties in power want to stay in power. One way to do that is to encourage politicians in their party to support things their constituents want and need. Things like safety. Good schools. A clean environment. Good roads. Stable, well-paying jobs.

But sometimes political parties do more than that. They may redraw the boundaries of voting districts to make it much more likely that their supporters will win a majority. This is gerrymandering — the drawing of voting-district boundaries in such a way that one party gets a deliberate edge.

The practice goes back to at least 1812. That year, Massachusetts governor Elbridge Gerry’s team drew up a state voting map. One oddly shaped district looked like a fantasy monster. A Boston newspaper called it the “Gerry-mander.” And so the term was born.

Each state sets its districts for picking state and federal lawmakers. Districts should have roughly equal numbers of voters. In general, those voters should all live in the same neighborhoods or communities. Districts shouldn’t be drawn on the basis of factors such as race. (In fact, drawing districts in a way that dilutes the votes of racial minorities has been ruled unconstitutional. Doing it in a way that prevents minorities from electing their preferred candidate is also illegal.)

Wisconsin’s plan basically met those tests. Still, the plan gave a statewide edge to Republican candidates.

In 2012, for example, Republicans running for the state’s lawmaking branch got 48.6 percent of the popular vote statewide, or just under five in every 10 votes. Yet of 99 seats, Republicans won slightly more than six in every 10.

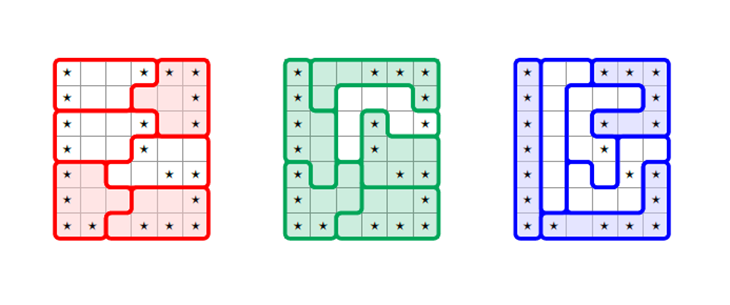
Like the original gerrymander, some voting districts may have odd — and tell-tale — shapes. But shape isn’t the only thing that matters. “You can do really unfair gerrymandering with shapes that look round and square and pretty,” Duchin notes. What’s more, oddly shaped districts might sometimes be fair.

“It’s not a beauty contest,” she says. Duchin and Mira Bernstein, also a mathematician at Tufts, wrote about the Wisconsin case and math in the October 2017 Notices of the American Mathematical Society.

Lawyers for both Maryland and Wisconsin did not want the courts to interfere. Maryland’s governor had even admitted that part of the reason for the challenged change was to give the Democrats an edge. Lawyers defending Wisconsin argued that voters could not challenge a statewide plan.

Story continues below image.

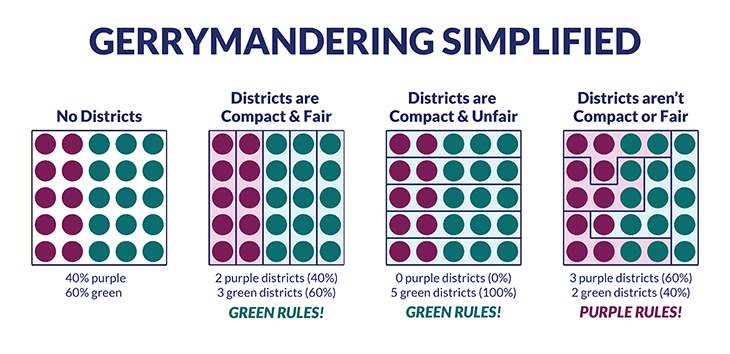
Cracking and packing

Math experts analyzed the Wisconsin state plan for the challengers. And those math experts found that two tricks led to gerrymandered vote results.

They refer to the first as “cracking.” It splits up a party’s supporters so they will be a minority in all or most districts. Their candidates might therefore lose in those places. The second trick is “packing.” It lumps a whole lot of one party’s backers into the same district. Now, their party’s candidate should win by a huge margin. However, many of the extra votes would be wasted; they wouldn’t affect the outcome of the election.

To see how cracking and packing can hurt, Duchin says, imagine a map with 42 grid squares. You want to divide it into six voting districts. Asterisks mark grid squares where voters prefer party X. Blank grid squares contain voters for party Z. If each party has 21 of the 42 squares, then you might expect each party to win in three districts.

But lines can be drawn to give one party’s supporters enough more than half the votes in most districts. Then party X might get five seats in the legislature, leaving Party Z with only one.

In an earlier case, the Supreme Court ruled that election results don’t have to match the proportion of voters statewide. Also, in real life, voters from different parties aren’t spread out evenly across a state. In some states, for example, people in large cities may be more likely to vote for Democrats. Republicans may be more common in rural areas. Social scientists ascribe such differences to what they call “political geography.”

Voters in both parties always have some “wasted” votes. Some votes will go beyond those needed for a candidate win. Other “wasted” votes would be votes for the losing side.

Adding to the problem: Not everyone votes. If one party is more likely to stay home on Election Day, their nonvoters may throw away the chance for their preferred candidate to win.

In 2012, 2014 and 2016, Wisconsin’s Democrats were significantly more likely to have “wasted” votes, the challengers said. In their view, that created an “efficiency gap.” Basically, they argued, the Republicans’ votes counted more than the Democrats’ did. In fact, Republicans did win a share of seats in the legislature that was far bigger than their statewide share of voters.  

Story continues below image.

Now the Supreme Court has said that the individual voters in Wisconsin can’t challenge the statewide voting district map. Rather, a voter can only claim harm based on his or her district. “An individual voter in Wisconsin is placed in a single district,” Chief Justice John Roberts wrote. “He votes for a single representative.” If there’s a problem, then the solution is to change the boundaries of that district, not all the districts in the state.

Scouting for gerrymandering

The decision will make it tougher to challenge state voting district plans. But the court left open the chance for people to prove that their votes were watered down. And it doesn’t prevent voters from raising different arguments in future suits. But first, plaintiffs will need to show that their district’s lines were drawn unfairly.

In Duchin’s view, you need a range of math tools to do that.

Among them: computers. Algorithms are groups of rules to solve a problem in a series of steps. Using them, computers can come up with many thousands of possible ways to divide a state map into voting districts. Those computer techniques can also suggest many, many ways to split up the actual distribution of voters. (Remember, people are not equally distributed across a state.) All those other district maps form a huge sample set of plans. Then, Duchin says, you can compare plans and how fairly they would represent all voters.

Another important tool: statistics. In this field of mathematics, researchers study sets of data and information that can be gleaned from them. An outlier is a datum, a single piece of data, that is well outside the range of the rest of the set. It can be either higher or lower than those other data. But in any case, it’s not what you’d otherwise expect from a random sample.

Outliers happen. But they raise questions in voting rights cases.

One question: Compared with other possible plans, does the outlier plan give members of one political party a significant advantage or disadvantage? “If your plan performs the way lots and lots of other plans would, then it’s presumptively okay,” Duchin says. But if it waters down the value of votes from one party, compared with the other, “then your plan is really an abusive outlier,” she suggests. In other words, it would suggest someone went out of their way to hurt or help one party.

Random switches

Wesley Pegden is a mathematician. He works at Carnegie Mellon University in Pittsburgh, Pa. His testimony about gerrymandering helped persuade judges to find that Pennsylvania’s congressional election map could not stand under state law. On March 19, the Supreme Court refused to block the new district map.

Like Duchin, Pegden likes the idea of seeing how voting district maps compare with other possible plans. But he suggests a different way to get a good sample of what other mapped districts would look like. His approach: Start with the plan that was drawn up. Then make random switches. At each step, pull a voting precinct (part of a district) in from a neighboring one, or give it up to a neighbor. This will create a whole lot of maps based on those small random changes.  

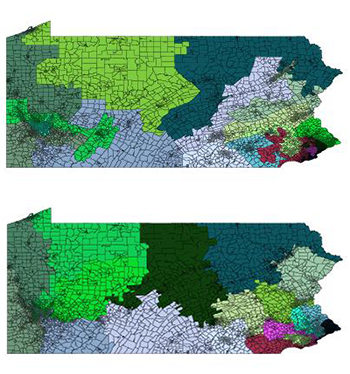
Then see how those new maps compare to the one that politicians drew up. So, Pegden would ask: If one party was at a big disadvantage in the politicians’ plan, does its handicap get bigger, smaller or stay pretty much the same as random changes are made to produce new maps?

Here’s a way to think about it, Pegden explains. Suppose you were asked to write numbers from one to 10 anywhere on a grid of squares. But you also want to make sure that any square someone might pick at random will be surrounded by squares with higher numbers. You can’t do it, Pegden says.

Likewise, when it comes to voting districts, “it is impossible,” Pegden says, for a series of random changes to map out new districts where each is fairer than the first — unless that first one had not been fair. That’s true regardless of an area’s political geography or other features, he notes.

Suppose almost all those maps made from little random-step changes would give election results with less bias for one party over the other. “Then that shows you that somebody worked hard to make that [first] map how it is,” Pegden says. And, presumably, the map produced by all of that hard work is unfair. His team wrote about the math and gerrymandering in the March 14, 2017 Proceedings of the National Academy of Sciences.

How could you draw districts that would be fair? Pegden and another group he works with suggest one approach. It’s like the “I cut, you choose” way to split a piece of cake. Under the plan, one party could “cut” the state’s area into districts. The other party could freeze the boundaries of one of those districts. Next, that other party could redraw all the other district lines. Now the first party would freeze one district’s lines. The process would go on until all the districts were frozen. The group plans to publish its work in a journal soon.

If an individual district was unfairly set, the Supreme Court said the remedy would be to change that district. But remember that districts need to have roughly equal numbers of voters. And the redrawn districts would have to avoid any legal problems that the first ones had. So it’s possible that challenges to enough single districts could lead to big changes in state maps.

Also, the courts are not the only place to work out complaints about voting district maps. 

Voters can ask state lawmakers to change the way they set districts. Voters can also push to amend a state’s constitution.

The gerrymandering issue shows the importance of math “for everyday basic problems,” such as how to hold fair elections, Pegden adds. “It’s important for us all to feel like government in a democracy is basically fair,” he says.