An ‘einstein’ shape eluded mathematicians for 50 years. Now they found one
The shape can cover an infinite area with a pattern that never repeats
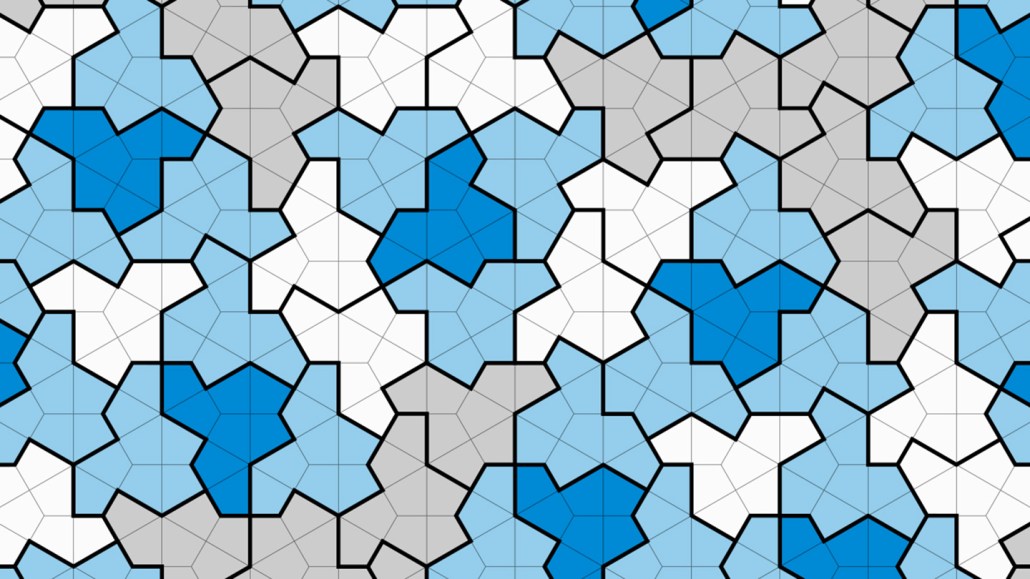
A 13-sided tile called “the hat” can fully cover an infinite plane. The tile’s pattern never repeats, making it an example of a long-sought shape known as an “einstein.” A small sample of that pattern is shown here.
D. Smith, J.S. Myers, C.S. Kaplan and C. Goodman-Strauss (CC BY 4.0)
To find a new, special type of shape, mathematicians put on their thinking caps.
In March, one team of them reported its success: a 13-sided shape that looks like a hat.
This hat was the first true example of an “einstein.” That’s the name for a special type of shape that can tile a plane. Like bathroom floor tile, it can cover an entire surface with no gaps or overlaps. It can even tile a plane that’s infinitely big. But an einstein tile does so with a pattern that never repeats.
“Everybody is astonished and is delighted, both,” says Marjorie Senechal. She’s a mathematician at Smith College in Northampton, Mass. She was not involved with the discovery. This ends a 50-year search for such a shape. “It wasn’t even clear that such a thing could exist,” Senechal says of the einstein.
The name “einstein” doesn’t refer to the famous physicist, Albert Einstein. In German, ein Stein means “one stone.” That refers to using a single tile shape. The hat sits weirdly between order and disorder. The tiles fit neatly together and can cover an infinite plane. But they are aperiodic (AY-peer-ee-AH-dik). That means the hat can’t form a pattern that repeats.
Infinite without repeating
Think about a tiled floor. The simplest ones are made with one shape that fits together neatly with others like itself. If you use the right shape, the tiles fit together with no gaps and no overlaps. Squares or triangles work well. You could cover an infinitely large floor with them. Hexagons also show up on many floors.
Floor tiles are typically arranged in a periodic, or repeating, pattern. You could shift the tiles over by one row and your bathroom floor would look exactly the same.
The hat could also cover an infinitely large floor. But it won’t form a pattern that repeats, no matter how hard you try.
David Smith identified the hat. He does math as a hobby, not as his job. He describes himself as an “imaginative tinkerer of shapes.” He was part of a team of researchers that reported the hat in a paper posted online March 20 at arXiv.org.
The hat is a polygon — a 2-D shape with straight edges. It’s surprisingly simple, says Chaim Goodman-Strauss. Before this work, if you’d asked him what an einstein would look like, he says, “I would’ve drawn some crazy, squiggly, nasty thing.” Goodman-Strauss is a mathematician. He works at the National Museum of Mathematics in New York City. He teamed up with Smith and other mathematicians and computer scientists to study the hat.
Mathematicians previously knew of tilings that couldn’t repeat. But all used two shapes or more. “It was natural to wonder, could there be a single tile that does this?” says Casey Mann. He’s a mathematician at the University of Washington Bothell. He was not involved with the discovery. “It’s huge,” he says of the hat finding.
From hat to vampire
The researchers proved that the hat was an einstein in two ways. One came from noticing that the hats arrange themselves into larger clusters. Those clusters are called metatiles.
Metatiles then arrange into even larger supertiles, and so on. This approach revealed that the hat tiling could fill an entire infinite plane. And it showed that its pattern would never repeat.
The second proof relied on the fact that the hat is part of a family of shapes that are also einsteins. You can gradually change the relative lengths of the sides of the hat. If you do that, you can find other tiles that can take on the same nonrepeating pattern. The scientists studied the relative sizes and shapes of the tiles at the ends of that family. At one end there was a tile shaped like a chevron. At the other end was a shape that looked a bit like a comet. Comparing those shapes showed that the hat couldn’t be arranged in a periodic pattern.
The work has yet to be peer-reviewed. That’s the process in which other experts in a field read and critique the work. But the experts interviewed for this article think that the result will likely hold up.
Similar tilings have inspired artwork. The hat appears to be no exception. Already the tiles have been made to look like smiling turtles and a jumble of shirts and hats.
And the hat wasn’t the end. In May, the same team made another announcement. They found a new type of einstein shape. This one is even more special. The researchers shared it May 28 in a paper at arXiv.org.
The first einstein made a pattern that involved both the tile and its mirror image. The new tile also makes a pattern that never repeats, but without its reflection. Because the shape isn’t paired with its reflection, you might call it a “vampire einstein,” the researchers say. They found a whole family of vampire einsteins that they’re calling “spectres.”
“I would never have predicted that we’d stumble upon a shape that solves this [vampire-einstein problem] so quickly,” says team member Craig Kaplan. He’s a computer scientist at the University of Waterloo in Canada.
Researchers should continue the hunt for einsteins, he says. “Now that we’ve unlocked the door, hopefully other new shapes will come along.”
