Experiment: Measure the speed of light with a laser
Think it takes expensive, sophisticated equipment to measure light speed? Think again!

You can measure the speed of light using just a laser pointer and a container filled with gelatin.
EThamPhoto/The Image Bank/Getty Images
Share this:
- Share via email (Opens in new window) Email
- Click to share on Facebook (Opens in new window) Facebook
- Click to share on X (Opens in new window) X
- Click to share on Pinterest (Opens in new window) Pinterest
- Click to share on Reddit (Opens in new window) Reddit
- Share to Google Classroom (Opens in new window) Google Classroom
- Click to print (Opens in new window) Print
Objective: Measure the speed of light in gelatin using a laser pointer
Areas of science: Physics
Difficulty: Easy advanced
Time required: 6–10 days
Prerequisites: Basic understanding of optics and trigonometry
Material availability: Readily available
Cost: $20–$50
Safety: Adult supervision is recommended. Even low-power lasers can cause permanent eye damage. Please carefully review and follow the Laser Safety Guide.
Credits: Shijun Liu, Science Buddies; Harvey Lynch, Stanford Linear Accelerator Center (SLAC)
The law of refraction, which is also known as Snell’s law, actually applies to everyday life. For example, when you see your friend’s face through the window, you’re seeing light that is refracted through the glass. Snell’s law describes what happens to the trajectory of a beam of light as it passes from one medium, such as air, to another, such as glass.
As you apply Snell’s law and the definition of index of refraction in this science project, you will be able to measure the speed of light in gelatin. The beauty of this science project also lies in how you can verify one of the most basic laws of optics, experimentally, by using readily available and inexpensive materials.
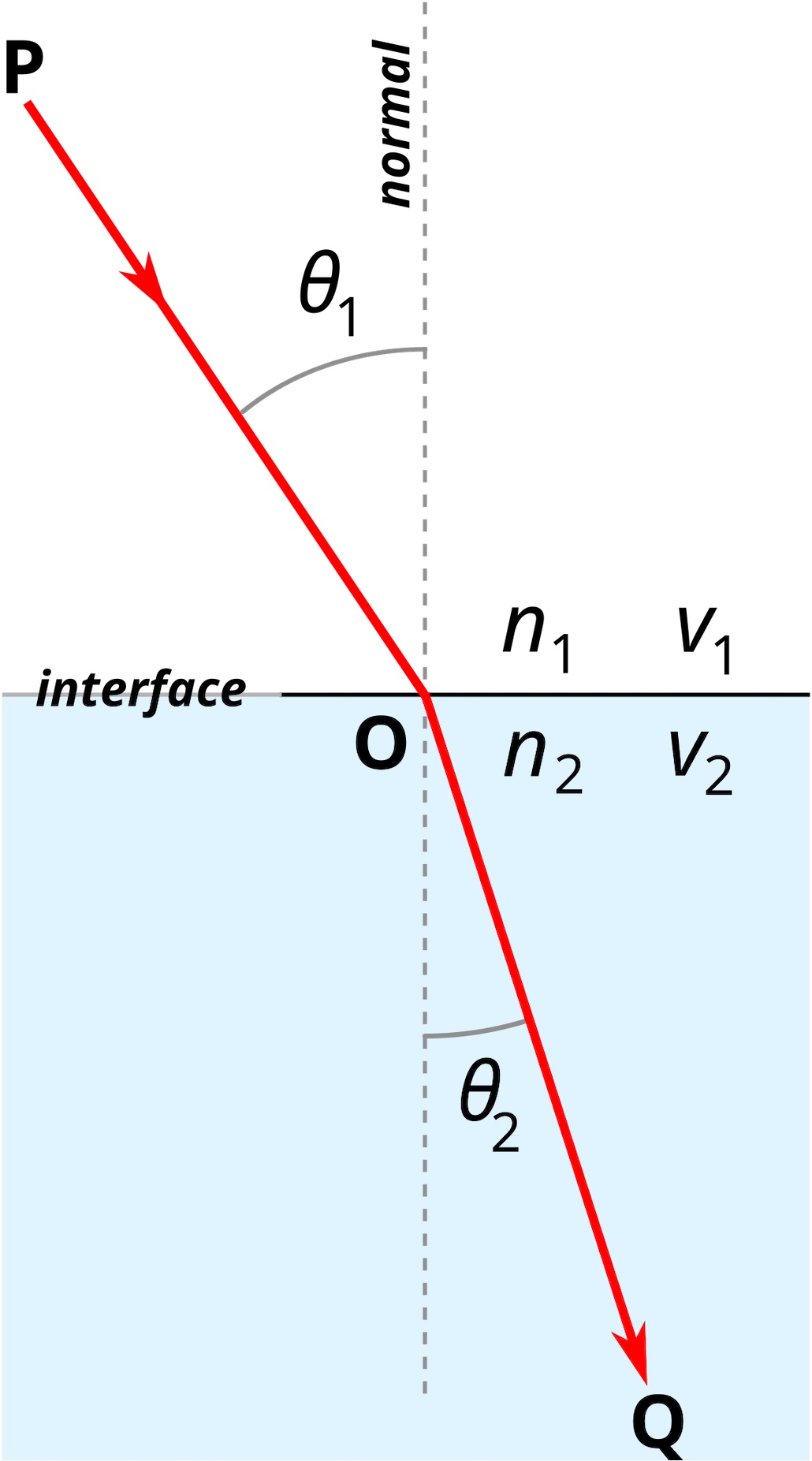
Snell’s law is expressed as the following equation (see Figure 1 below for an illustration of the variables):
Equation 1:
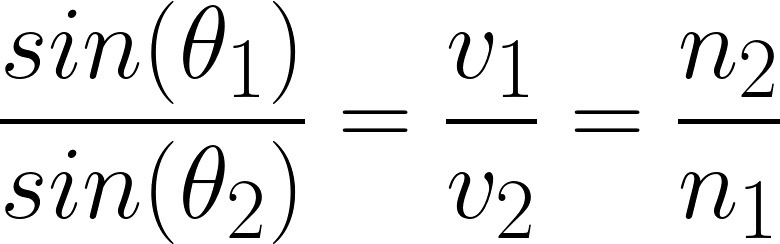
- θ1 is the angle between the incident light beam and the surface normal
- θ2 is the angle between the departing light beam and the surface normal
- v1 is the speed of light in the first material (in this project, air)
- v2 is the speed of light in the second material (in this project, gelatin)
- n1 is the index of refraction of the first material (in this project, air)
- n2 is the index of refraction of the second material (in this project, gelatin)
Note that Snell’s law not only applies to the case of the laser beam passing through air and gelatin, but also to other examples of how the incident object changes direction as it passes from a faster medium to a slower medium, and vice versa.
For example, a marching band walks together in time with the music and takes the same-length steps. What if the band moves across a grassy football field at an angle, and as each band member crosses the 50-yard line, he or she suddenly finds the field very muddy and slippery? As a result, he or she steps in time but takes steps that are 20 percent shorter because of the mud. What happens then? Answer: Those who have crossed the 50-yard line are traveling at 80 percent the speed of those who have not, and the line of band members bends at the 50-yard line, just like light in this experiment. With a little thought, one can even compute the angle at which the line bends (actually the reverse of what you will be trying to do in this science project).
Terms and concepts
- Law of refraction (also called Snell’s law)
- Trajectory
- Index of refraction
- Incident object
Questions
- What exactly is a laser?
- What is the speed of light? What are some methods scientists have used to calculate it?
- What are some applications of Snell’s law?
Resources
This resource provides more information about lasers:
- Wikipedia Contributors. (2010, July 6.) Laser. Wikipedia: The Free Encyclopedia. Retrieved July 12, 2010, from http://en.wikipedia.org/w/index.php?title=Laser&oldid=371975776.
To learn more about Snell’s law, try these links:
- Wolfram Research. (n.d.). Snell’s Law. Retrieved July 12, 2010, from http://scienceworld.wolfram.com/physics/SnellsLaw.html.
- Kaiser, Peter K. (n.d.). Snell’s Law. Retrieved July 12, 2010, from http://www.yorku.ca/eye/snell.htm.
- Nave, R. (n.d.). Snell’s Law. Retrieved July 12, 2010, from http://hyperphysics.phy-astr.gsu.edu/hbase/geoopt/refr.html#c3.
- The Physics Classroom. (n.d.). The Mathematics of Refraction: Snell’s Law. Retrieved July 12, 2010, from http://www.physicsclassroom.com/Class/refrn/u14l2b.cfm.
The links below contain additional information about the index of refraction:
- Reed, R. (n.d.). Refraction of light. Retrieved July 12, 2010, from http://interactagram.com/physics/optics/refraction/.
- Wolfram Research. (n.d.). Index of Refraction. Retrieved July 12, 2010, from http://scienceworld.wolfram.com/physics/IndexofRefraction.html.
- Nave, R. (n.d.). Index of Refraction. Retrieved July 12, 2010, from http://hyperphysics.phy-astr.gsu.edu/hbase/geoopt/refr.html#c2.
Materials and equipment
- A device that produces a visible laser beam, such as a laser pointer or a laser level (for example, search for “laser pointer” at Amazon.com).
- Many kinds of lasers are readily available on the market. Typically, lasers are classified by their wavelength and maximum output power, which put them into one of several classes, e.g., class I, II, IIIa, IIIb, IV (see Laser Safety Guide). When handling lasers, please keep in mind the safety measures that must be followed in order to prevent injuries.
- A mounting device on which the laser device rests that can easily indicate where the beam is pointed (it will be difficult to actually see the laser beam passing through air).
- A protractor or a homemade protractor that can easily indicate the angle of refraction inside the gelatin.
- Gelatin (a clear or a light/transparent color generally works best).
- Plastic containers to mold the gelatin (of various shapes and sizes if pursuing one of the possible variations below).
Experimental procedure
Below is an outline of one way to carry out the experiment. There are multiple variations and points where you can insert your own creativity (see below):
1. First, come up with your own experimental setup. In addition to understanding the theory behind the experiment, this project calls for some experimental design creativity and hands-on “playing time.”
Think about how one would measure the angle of incidence of a laser passing through the gelatin, with reference to the normal (the line that is perpendicular to the surface of the medium). Also consider how one could precisely direct the laser beam from the laser pointer (or laser level) at a predetermined “entry point.” What type of mounting structure would you come up with?
For example, the photo below (using a tub of liquid instead of gelatin) represents a clever setup. The laser beam was originally along the line between the tiles on the countertop (you could also use graph paper). You can see a bit of the beam exiting the laser in the center of the circle, and you can see the entry point of the laser in the plastic container. These two points show the original path of the beam, and you can easily connect the points to create the original trajectory. (Note that the normal, which is not shown, is the line that runs perpendicular to the side of the plastic container that gets hit by the laser.) Thus, we can accurately measure the angle here.

2. Make your gelatin according to the directions on the box. Remove the gelatin from the container when it has set.
- Note: Try to make the gelatin in a square container (like the container shown in the photo above). If a square container is not available, use a large container and cut the gelatin in a square or “box” shape with edges that are clean and vertical. Slanted and uneven edges may cause disruption of the laser beam, so it is important that the form of the gelatin be correct.
- Note: The gelatin can be deformed if you are not careful when removing it from the container — or deformed by the tools you use to remove it. One way to remove the gelatin from the container is to set the container in hot water and let it float on the surface for a bit. This softens the edges of the gelatin inside the container, allowing you to turn the container upside-down to release the gelatin. Having the gelatin out of the container gives a clean optical interface, but gelatin may not stay straight once it is out of the mold. If the sides bulge significantly, the angles will be distorted.
3. Mount the laser pointer on a premade device that will indicate where the beam is going and what the angle of incidence is (recall that it will be difficult to actually see the laser beam passing through air).
- Note: It is important that the laser beam be perpendicular to the surface for proper refraction results.
4. Fix the laser device and record the angle of incidence with respect to the normal.
5. Shine the laser through the gelatin. (You may need another person to help out by holding down the button if you use a simple laser pointer.) Measure the angle of refraction inside the gelatin.
- Note: Measuring the angle from the normal can be tricky. One must remember that if one looks directly into a refracting medium, i.e., perpendicular to the surface, the angles are accurate, but if one looks off the normal, the angles are distorted. For example, a straight stick thrust into water looks broken at the surface. Therefore, it is important to set up the angle measuring device properly so accurate readings can be obtained.
6. Find the speed of light in gelatin: First, use Snell’s law (refer to the introduction) to calculate the index of refraction of the gelatin. Then apply the definition of index of refraction to find the speed of light in the medium.
Variations
There are many areas of this project where one can use their own creativity:
- Laser mounting device. Make your own device to ensure that the laser beam precisely enters the gelatin at the predetermined entry point.
- Measuring scheme for the angle of refraction. Design your own scheme to measure the angle of refraction inside the gelatin. For example, where would you place a custom-made protractor to indicate the angle of refraction with respect to the normal?
- Faster or slower gelatin. Attempt to change the index of refraction of the gelatin and create “faster” or “slower” media. For example, what happens when one dissolves various amounts of sugar in a well-mixed gelatin solution? Does the index of refraction of the gelatin change? Consequently, how does the speed of light in gelatin change? Note that one can represent the concentration of the sugar-gelatin solution by doing a one-step percent composition by mass calculation, which is basically the mass of the solute divided by the mass of the solution (mass of solute plus mass of solvent), multiplied by 100.
For example: Determine the percent composition by mass of a 100 g salt solution which contains 20 g salt.
Solution: 20 g NaCl / 100 g solution x 100 = 20 percent NaCl solution
From the table shown below, we see that the index of refraction for a 30 percent sugar solution is 1.38 and for an 80 percent solution is 1.49. Can you verify a positively correlated trend for sugar?
- Other readily available materials. Calculate and verify the indices of refraction of other readily available materials like household liquids or ice. For example, ethyl alcohol has an index of refraction of 1.36, while ice’s is 1.31. Can you verify this? A table of indices of refraction for commonly found materials is shown below. Note that extra caution must be taken if you are using a plastic container to hold the liquid as the container itself serves as an interface between the laser and the media. Think about ways to minimize this distortion. For example, can you try to aim the laser at the surface of the liquid (at an angle with respect to the normal) from above? How would you measure the angle?
- Make lens cross-sections out of gelatin, then “ray trace” with the laser. Basically, ray tracing involves establishing the position and orientation of an object’s image by tracing strategic rays of light from the object passing through the lens, using knowledge of the focal length of the lens and the position of the object. Here is an introduction: http://boson.physics.sc.edu/~rjones/phys153/raytrace.html.
| Material | Index |
| Vacuum | 1.0 |
| Air at standard temperature and pressure | 1.00029 |
| Ice | 1.31 |
| Water at 20 °C | 1.33 |
| Acetone | 1.36 |
| Ethyl alcohol | 1.36 |
| Sugar solution (30%) | 1.38 |
| Fluorite | 1.433 |
| Fused quartz | 1.46 |
| Glycerine | 1.473 |
| Sugar solution (80%) | 1.49 |
| Plexiglass | 1.51 |
| Crown glasses | 1.52-1.62 |
| Sodium chloride | 1.54 |
| Polystyrene | 1.55-1.59 |
| Carbon disulfide | 1.63 |
| Flint glasses | 1.57-1.75 |
| Methylene iodide | 1.74 |
| Sapphire | 1.77 |
| Rare earth flint | 1.7-1.84 |
| Lanthanum flint | 1.82-1.98 |
| Arsenic trisulfide glass | 2.04 |
| Diamond | 2.417 |
| Gallium phosphide | 3.5 |
This activity is brought to you in partnership with Science Buddies. Find the original activity on the Science Buddies website.








