Math predicts weird materials; leads to 2016 physics Nobel
Prize recognizes three researchers working in a type of math called topology

David Thouless, Duncan Haldane and J. Michael Kosterlitz (left to right) will share the 2016 Nobel Prize in physics. The award recognizes their theoretical discoveries on exotic states of matter. Their work was based on the mathematics of topology.
From left: ©Trinity Hall, Cambridge, Photographer Kiloton Howard; Denise Applewhite/Office of Communications/Princeton University; Johanna Lassy/Aalto University
Share this:
- Share via email (Opens in new window) Email
- Click to share on Facebook (Opens in new window) Facebook
- Click to share on X (Opens in new window) X
- Click to share on Pinterest (Opens in new window) Pinterest
- Click to share on Reddit (Opens in new window) Reddit
- Share to Google Classroom (Opens in new window) Google Classroom
- Click to print (Opens in new window) Print
Three physicists won the 2016 Nobel Prize in physics for discoveries about exotic states of matter. Their work was theoretical. That means it was based on mathematical calculations, not on tests in a lab or on observations in nature.
On October 4, the Nobel committee in Stockholm, Sweden announced the three winners. David Thouless is at the University of Washington in Seattle. J. Michael Kosterlitz works at Brown University in Providence, R.I. Duncan Haldane is at Princeton University in New Jersey.
Their work is “fairly abstract,” notes Princeton’s M. Zahid Hasan. “It’s not like finding a new particle,” this physicist explains. “It’s about how ordinary matter can behave in extraordinary ways.” Clearly, he says, this award is “deserving” for the trio’s important work.
All three worked in a branch of mathematics that deals with the study of shapes. It is known as topology. Their discoveries spurred interest in creating what have come to be called topological materials.
Potential uses for such materials include quantum computing and new types of computer hard drives.
Thinking about bread
In topology, different shapes are distinguished by abrupt transitions. Consider the holes found in some breads. A loaf of bread has no holes in it. To create a bagel shape, one needs to cut out a hole. A pretzel with two holes can be made from a looped cord of bread. But to morph from the bread loaf shape into a bagel or looped pretzel, a baker needs to introduce a hole or two. That makes each shape, from a topological point of view, quite different.
One of these shapes cannot be gradually turned into the other without cutting parts. But anything with the same basic shape — one hole, two holes or no holes — will be twins. That’s true, at least, from a topological point of view. So as hard as it may be to imagine, by this way of reasoning a bagel and a coffee cup are twins. After all, each has a single hole: The bagel’s is in the middle and the coffee cup’s is in its handle.
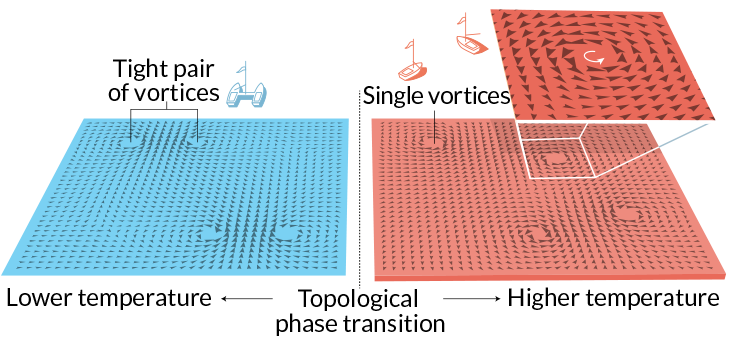
Using concepts from this type of math, the researchers worked to probe extreme states of matter. Most people know the basic states: solid, liquid, gas and plasma. With a phase change, a material may morph from one to another of these. But under extreme conditions — such as temperatures near absolute zero — materials can behave oddly. Now the physics of quantum mechanics takes over. Superconductors are one such quantum state. Here, electricity flows with no resistance.
Research by this year’s Nobel winners predicted new phenomena that might come to life in such a quantum world. And indeed, such oddities eventually did show up.
In recent years, topological materials have become one of the hottest topics in physics. One widely studied example: topological insulators. These are materials that can serve simultaneously as both electrical insulators — blocking the flow of a current — and conductors of an electrical current.
Suddenly, people are realizing that topological effects “are just a tremendously rich subject,” said Haldane. The Princeton-based winner offered this assessment by phone during the announcement of his prize.
He and his co-winners “certainly were the first people to emphasize the role of topology in physical phenomena,” says Laurens Molenkamp. He’s an experimental physicist. He works at the University of Würzburg in Germany. The scientists named today, he says, “certainly deserve a Nobel Prize.”
What they did
A two-dimensional material has length and width but no height. Thouless and Kosterlitz made discoveries about phase changes in such 2-D materials. Everyone is familiar with certain phase changes. Ice melting into water is one of the best known. Exotic quantum materials also exhibit phase changes, where their properties suddenly shift. But theirs are far less easy to imagine than the change from ice to water.
For instance, this pair of scientists discovered a new phase change that occurs at very low temperatures. Named for them, this Kosterlitz-Thouless transition occurs with the behavior of tornado-like vortices of swirling electrons. Those swirls pair up and are locked together. If the temperature warms, however, these vortices will suddenly separate. Afterward, each will travel on its own. Eventually, experimental scientists witnessed this happening in very thin films of superfluid helium and with superconductors.
In 1983, Thouless used topology to explain another mysterious phenomenon that had been seen in tests. It is known as the quantum Hall effect. The effect develops within a thin layer of electrically conducting material. It was initially seen only when the temperature was extremely cold and a high magnetic field was present. Under such conditions, the electrical conductivity of a layer would change. But it didn’t happen gradually. Instead, the changes took place in regular jumps. The move from one phase to another occurred at integer multiples. As the magnetic field changed, for example, the conductivity changed. But instead of shifting gradually, it happened in discrete jumps, perhaps changing to double or triple its initial value.

Thouless showed how this effect was related to topology. Consider the bread loaf, bagel and pretzel again. The loaf has no hole, the bagel has one and the slightly looped pretzel has two. Their number of holes varies by a whole number. It can’t vary by a fraction. There is no bread with one-and-a-half holes, or two-and-a-third holes. So any change in the number of holes can vary only in integer leaps — just as the conductivity changes in the quantum Hall effect. (In 1988, Haldane showed that a similar effect can occur even in the absence of a magnetic field.)
Haldane also predicted a new behavior in chains of atoms.
Atoms in the chain each have a quantum property. Scientists refer to this as spin. It makes the chains behave like tiny magnets. In this case, the spins can occur as an integer or a half integer. A chain with integer spin will behave differently than one with half-integer spin, Haldane showed.
Why scientists care about these odd traits
The three new Nobelists “laid a foundation for the way that we think about materials and matter,” says Charles Kane. He’s a physicist at the University of Pennsylvania in Philadelphia. Their findings have profound implications, he says. The effects can be seen “from our understanding of the phenomenon of superconductivity to our understanding of the electronic structure of materials.”
Their work also has inspired new topological materials. For instance, those topological insulators may carry current on their surface, while barring the flow of electricity inside. Or they might prevent light from flowing through a piece of etched glass but allow that light to flow well along its surface.
The research behind such materials has “combined beautiful mathematical and profound physics insights,” said Thors Hans Hansson during the Nobel announcement. Hansson is a physicist at Stockholm University. He is also a member of the Nobel committee for physics. Importantly, he noted, the winners’ mathematical predictions were later “confirmed by experiment.”
The three men will share 8 million Swedish kronor (or about $934,000). But it won’t be divided equally. At a December 10 ceremony in Stockholm, Thouless will receive half of the total. Kosterlitz and Haldane will split the rest.
Their prize is named for Alfred Nobel. Best known as the inventor of dynamite, he was a wealthy man when he died on December 10, 1896. In his will, Nobel left much of his fortune to create prizes to those who have done their best for humanity in the fields of physics, chemistry, physiology or medicine, literature and peace.
Note: This story has been revised to more accurately describe the quantum effects of spin in chains of atoms.







