Getting cozy with a science experiment
Tea cozies supposedly keep tea hotter longer, but do they really work?

This teapot (left) has a cozy on it. Does the cozy really help keep the tea inside warm? An experiment can find the answer.
CBCK-Christine/iStock/Getty Images Plus
Share this:
- Share via email (Opens in new window) Email
- Click to share on Facebook (Opens in new window) Facebook
- Click to share on X (Opens in new window) X
- Click to share on Pinterest (Opens in new window) Pinterest
- Click to share on Reddit (Opens in new window) Reddit
- Share to Google Classroom (Opens in new window) Google Classroom
- Click to print (Opens in new window) Print
This article is one of a series of Experiments meant to teach students about how science is done, from generating a hypothesis and designing an experiment to analyzing the results with statistics. You can repeat the steps here and compare your results — or use this as inspiration to design your own experiment.
There are lots of things that we do in our daily lives without questioning. Some people who drink tea, for instance, place a cozy over a teapot filled with the hot drink. A tea cozy is small cover made of some sort of fabric. Think of it as a teapot sweater to keep the tea warm for a longer period of time. But can one layer of fabric covering a boiling pot of tea really make a difference? I was skeptical. So I designed an experiment.
Hot water doesn’t stay hot. It cools over time.
Heat is energy flowing through a system. As water absorbs energy from another source, it heats up. The energy from the stove makes the molecules in the water move faster, which raises the water’s temperature. When water is poured into a teapot, some of its energy will move to the material in the pot through conduction. As speeding atoms in the water bounce against the sides of the pot, they transfer some of their energy. This warms the teapot and cools the tea slightly. The teapot, in turn, will transfer some of its heat to the air around it.
After an hour or two of losing energy to the teapot and surrounding air, the tea in the pot is no longer hot. It reaches equilibrium with the air, matching its temperature.
An insulator is a material that doesn’t transmit energy easily. One example is a blanket. It traps your body heat and keeps you warm. Similarly, a tea cozy should insulate a teapot, trapping energy inside and keeping the brew warm.
But most cozies are just yarn or fabric. If they’re knitted or crocheted, they’re full of holes! Could they possibly be that good an insulator?
This gave me a hypothesis — a statement that I could test: A teapot’s water will remain hot longer with a cozy than without, no matter what the teapot is made from.
To test that, we also should consider a null hypothesis — one that states there’s no effect of a tea cozy. If this were true, then any effect seen would be due to error. Here, the null hypothesis is: A teapot with a cozy will not keep water hot longer than a pot without a cozy, no matter what the teapot is made from.

Cozy studies
Not all teapots are the same. They can be made from different materials — such as glass, iron or some ceramic. I collected three similarly sized teapots: one each made of metal, glass and china.

Then, I crocheted a cozy for each pot. Crochet is a craft that makes fabric by hooking yarn with a needle. (If you want to repeat this experiment, you could knit, sew or quilt a cozy — or just buy one online.)
For my experiment, I didn’t bother making tea. I only needed boiling water. I used an electric kettle, but a stove-heated kettle or pot will work, too. Once the water was boiling, I took the temperature of the water with a digital thermometer. I placed 240 milliliters (one cup) of water into each teapot. Then I took the temperature of the water in each teapot. I put the lids on and set a timer. I took the temperature of the water again 15 minutes, 30 minutes, one hour and two hours after I had boiled the water.
The teapots weren’t yet wearing their cozies. This was just a control. I boiled water again, and took temperatures again. I did this five times with the teapots alone, and five times for each teapot in its cozy.
I ended up with a lot of data, which show how each teapot’s contents cooled over time. You can see them all here:
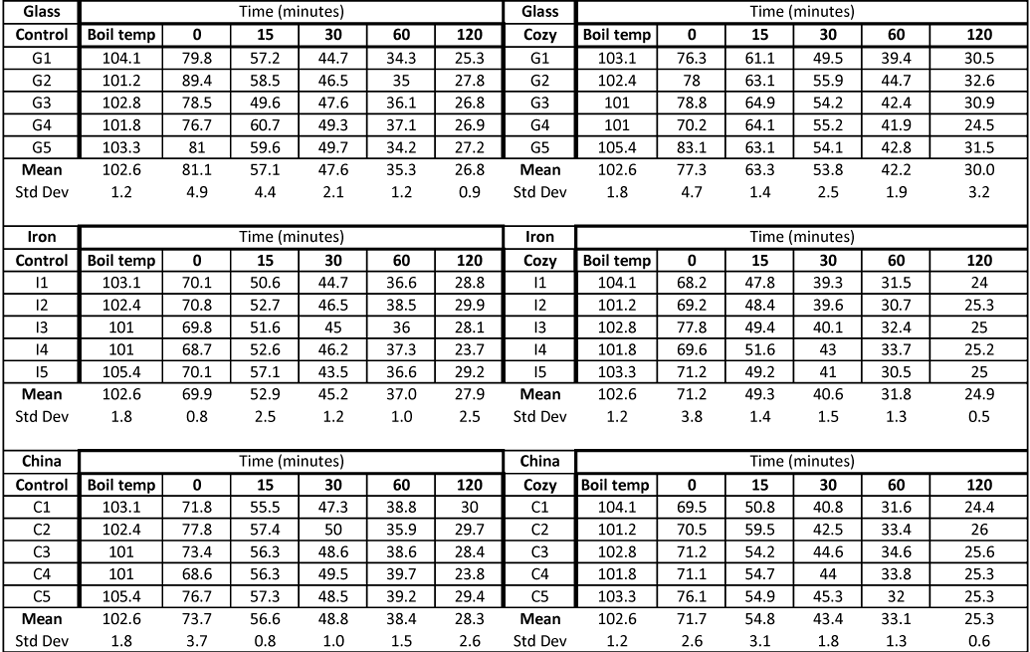
Here’s the tea
There are a few different ways to look at these data. Each involves different statistics — ways to analyze the numbers and interpret their meaning.
For all of these groups together, I can run something called an analysis of variance, or an ANOVA. This can tell me the difference between two variables — things that I’m testing. I used a trial of a program called Graphpad Prism to run this test. (Read the instructions carefully for whatever program you use.)
An ANOVA provides a p value, or measure of probability. The p value can tell me whether or not I would likely see a difference as big as or bigger than the one I found if the difference were due solely to chance. Usually, scientists consider a p value of less than 0.05 — or five percent — as statistically significant.
There are lots of types of ANOVA. Here, I wanted to run a repeated-subjects ANOVA. This test is used when the same subjects — or in this case, teapots — end up in both groups. I combined all of the data from the teapots with cozies into one group. Data from teapots without covers make up the second group.
Wow. When all the data are grouped together, it doesn’t look like there’s much difference. But I still need to run my ANOVA. It will give me a p value for the change in water temperature over time. It also will give me another p value comparing teapots with cozies to teapots without. Finally, it will give me a p value that measures if there is an interaction between the change in temperature over time and whether the teapot wore a cozy.
Results show a p value of 0.0001 for the effect of time. That means there’s one-hundredth of a percent chance that I would see a difference this big or bigger if no difference existed. This isn’t a surprise. I would expect the water in the teapots to cool with time.
I then got a p value of 0.4727 for the effect of the cozy. That is not anywhere close to statistically significant. It means that teapots with cozies were neither warmer nor colder than teapots without. Finally, I got a p value of 0.8265 for the interaction between the two. That means there’s no significant effect of the cozy on how fast the water in the teapots cooled.
It appears that my hypothesis was wrong. My data instead seem to prove the null hypothesis: that a teapot with a cozy will not keep water hot longer than a pot without one.
Am I disappointed? Not at all. Negative data are still data. They are still worth knowing. My tea cozies didn’t do what I intended. So I can save my yarn for something else.
There are all sorts of questions I could ask about why I didn’t find a difference. Perhaps the difference is small, and I didn’t boil enough pots of water to tease that out. I also had teapots of three different materials, and the first graphs shows that those materials might be cooling at different rates, with or without the cozies. I could run more experiments to test whether cozies work on only one type of teapot.
It’s also possible that some cozies are better than others. Maybe quilted or felt tea cozies work better than ones crocheted out of yarn. So I could design another experiment comparing all of those.
Finally, it’s possible that there’s no difference in how slowly the water cools — and people merely believed a difference is there. I could ask tea drinkers to rate the heat of tea from teapots with or without cozies. Negative data, such as mine here, may not show a difference. But they always offer the opportunity to ask more questions.
Final thoughts
Science News for Students published a version of this experiment last month. But a reader, Alan Colburn, of California State University in Long Beach, noticed an apparent problem. My numbers didn’t seem to add up, he wrote me. The averages for each time point in the control group did not match the averages in the data tables.
We took down the story, and I immediately went digging into those data. I found my mistake right away. I had copied and pasted data into my graphing program incorrectly. That affected the resulting graph and related statistics. I hadn’t noticed that error as I had been wrestling with the graphing program for a long time. But I was inclined to believe there was a difference. That bias — a belief I had about my potential results — meant I did not question my findings.
In scientific research, such a mistake might have been caught in peer review. That’s when other scientists in the field look over a paper before it is published in a scientific journal. They keep an eye out for mistakes such as this one.
Mistakes like this are embarrassing. They take time to correct. Thankfully, Colburn’s careful attention to detail kept me from mistakenly giving thousands of readers the wrong idea about what tea cozies can do. Telling the truth — in science and in journalism — is more important than any embarrassment I may have over a mistake.
Materials
- Measuring cups: $7.46
- 2 skeins of worsted weight yarn: $3.44/skein
- Handheld infrared thermometer: $18.00
- Glass teapot: $22.00
- Iron teapot: $22.00
- China teapot: $37.32
- Electric kettle: $19.96







