Experiment: M&M’S geometry
In this science project, M&M’S stand for measurements and models!

M&M’S candies have a bit of an odd shape. They're not exactly spherical. But they're not exactly disks, either. In this experiment, let's use mathematical models of different shapes to find out which one most closely matches M&M’S.
DebbiSmirnoff/iStock Unreleased/Getty Images
Share this:
- Share via email (Opens in new window) Email
- Click to share on Facebook (Opens in new window) Facebook
- Click to share on X (Opens in new window) X
- Click to share on Pinterest (Opens in new window) Pinterest
- Click to share on Reddit (Opens in new window) Reddit
- Share to Google Classroom (Opens in new window) Google Classroom
- Click to print (Opens in new window) Print
Objective: Investigate which formula is the most accurate for estimating the volume of an M&M’S candy
Areas of science: Math
Difficulty: Hard beginner
Time required: ≤ 1 day
Prerequisites: None
Material availability: Readily available
Cost: under $20
Safety: No issues
Credits: Sara Agee, Ph.D., Science Buddies; Teisha Rowland, Ph.D., Science Buddies; M&M’S® is a registered trademark of Mars, Inc.
Geometry is the study of how to use math to describe and investigate different points, lines and shapes. The way that a shape is described in geometry is with a formula, which is simply a mathematical way to calculate different properties of a shape like size, area or volume. Volume is a unique property of three-dimensional shapes, because three-dimensional shapes take up space in three different directions. Most real-world objects are three dimensional: balls, cars, food, etc.
The problem with geometric formulas is that they describe “perfect” or “ideal” shapes. A sphere is an “ideal” three-dimensional shape that is perfectly circular in all directions. Even though a ball is spherical in shape, it is not a perfect sphere. If geometric formulas describe “ideal” shapes and not “real” shapes, then how are they useful in the “real” world?
Most real-world shapes are not simple shapes and use complex geometry to be calculated. The properties of real-world shapes can also be approximated, or estimated, to the best possible measure with a geometric formula. This is called making a geometric model, and the most important part of making a good geometric model is choosing the formula that best describes the object. Even the most irregular objects can be modeled by using geometry: cars, airplanes, electronics, plastics, food, etc. Geometric modeling is very important for manufacturing because a product needs to have the same shape, made the same way, every time.
In this mathematics science project, you will use geometry to produce a mathematical model of an M&M’S candy. If you look closely, you will see that the volume of an M&M’S candy is a bit irregular. It is not quite perfectly round. It looks like a ball shape (sphere) that has been squished on one side, as shown in Figure 1. You will test three different formulas (one for a sphere, one for a cylinder and one for an ellipsoid) to see which formula makes the best geometric model of an M&M’S candy. You will test each formula by using it to calculate the volume of an M&M’S candy and then you will compare your result to the actual volume of a single piece of candy.

Terms and concepts
- Geometry
- Formula
- Volume
- Model
- Radius
- Diameter
- Height
- Sphere
- Cylinder
- Ellipsoid
Questions
- What is a geometric model? Why can it be useful?
- Which formula do you think will calculate the most accurate volume of an M&M’S candy? Why?
- How are geometric formulas different from each other?
- What other ways can you use geometric formulas to measure real-world objects?
Resources
For help creating graphs, try this website:
- National Center for Education Statistics, (n.d.). Create a Graph. Retrieved June 25, 2020.
Materials and equipment
- M&M’S (110). One 7-oz (198-g) bag holds about 210 M&M’S.
- Metric ruler that measures in centimeters (cm)
- Metric measuring glass or cup that measures in milliliters (mL). Must measure at least 200 mL.
- Water
- Table or countertop
- Piece of paper
- Clay or Play-Doh. Use a small amount that you do not mind ruining.
- Computer with Internet connection
- Lab notebook
Experimental procedure
- First, measure the actual volume of an M&M’S candy using a water displacement test.
- In your lab notebook, make a data table like Table 1. You will be recording your measurements in it.
- Fill the metric measuring glass or cup with 100 milliliters (mL) of water.
- Make sure it has exactly 100 mL. You can do this by looking at where the top of the water is when your eyes are level with it.
- Add 100 M&M’S to the water.
- Why do you think you are using 100 M&M’S instead of just one? Dropping just one M&M’S into a glass of water will not change the water level by much. By using 100 M&M’S you will be able to see a larger change in the water level that will be easier to measure. You can then divide the change you see for 100 M&M’S by the number 100 to calculate the volume of a single M&M’S candy.
- In the data table in your lab notebook, record the new, final volume of water.
- Estimate the new volume as closely as you can based on the marks on the glass. For example, if it is halfway between a mark that says “150” and one that says “175,” then you can estimate that it is at about 163 mL.
- Subtract the beginning volume of water (100 mL) from the new volume of water (that you just measured) to calculate the actual volume of the 100 M&M’S. Write this in your data table.
- To continue the example above, if the volume for 100 M&M’S is 163 mL, then you do this calculation: 163 mL – 100 mL = 63 mL. This means that 100 M&M’S have a volume of 63 mL.
- Divide your answer by 100. This is the actual volume of a single M&M’S candy in milliliters. Write this answer in your data table. You will be referring to this value later.
- In our example you would do this calculation: 63 mL / 100 = 0.63 mL, meaning that each M&M’S candy has a volume of 0.63 mL. Remember, this is just an example of the calculations. You will have to do the experiment yourself to see what the real volume is!
| Actual volume (mL) | |
| Starting volume (mL) | 100 mL |
| Final volume (mL) | |
| Actual volume of 100 M&M’S (mL) | |
| Actual volume of 1 M&M’S candy (mL) |
- Next you will test different mathematical formulas to see which one is the best geometric model of an M&M’S candy. Before doing this, make sure you do your background research and know what the terms radius, diameter, height, sphere, cylinder and ellipsoid mean.
- You will be making some careful measurements with (fresh!) M&M’S candies to use in the different formulas. In your lab notebook, make a data table like Table 2 to record your measurements in.
| Long side (cm) | Short side (cm) | |
| Diameter of 10 M&M’S | ||
| Diameter of 1 M&M’S candy (divide by 10) | ||
| Radius of 1 M&M’S candy (divide by 2) |
- Measure the long side of 10 fresh M&M’S lined up in a row. (Do not use any of the M&M’S that you used in the water displacement test!) Do this by using the following neat little trick:
- Place a piece of paper on a clean table or countertop.
- On top of the paper, place a small amount of clay or Play-Doh.
- Flatten it and stretch it out into a little line. Make it run along the length of the ruler.
- Line up 10 fresh M&M’S on their flat side, end to end, as shown in Figure 2. Poke them into some clay to keep them in a neat row with each M&M’S touching the next and no gaps in between them.
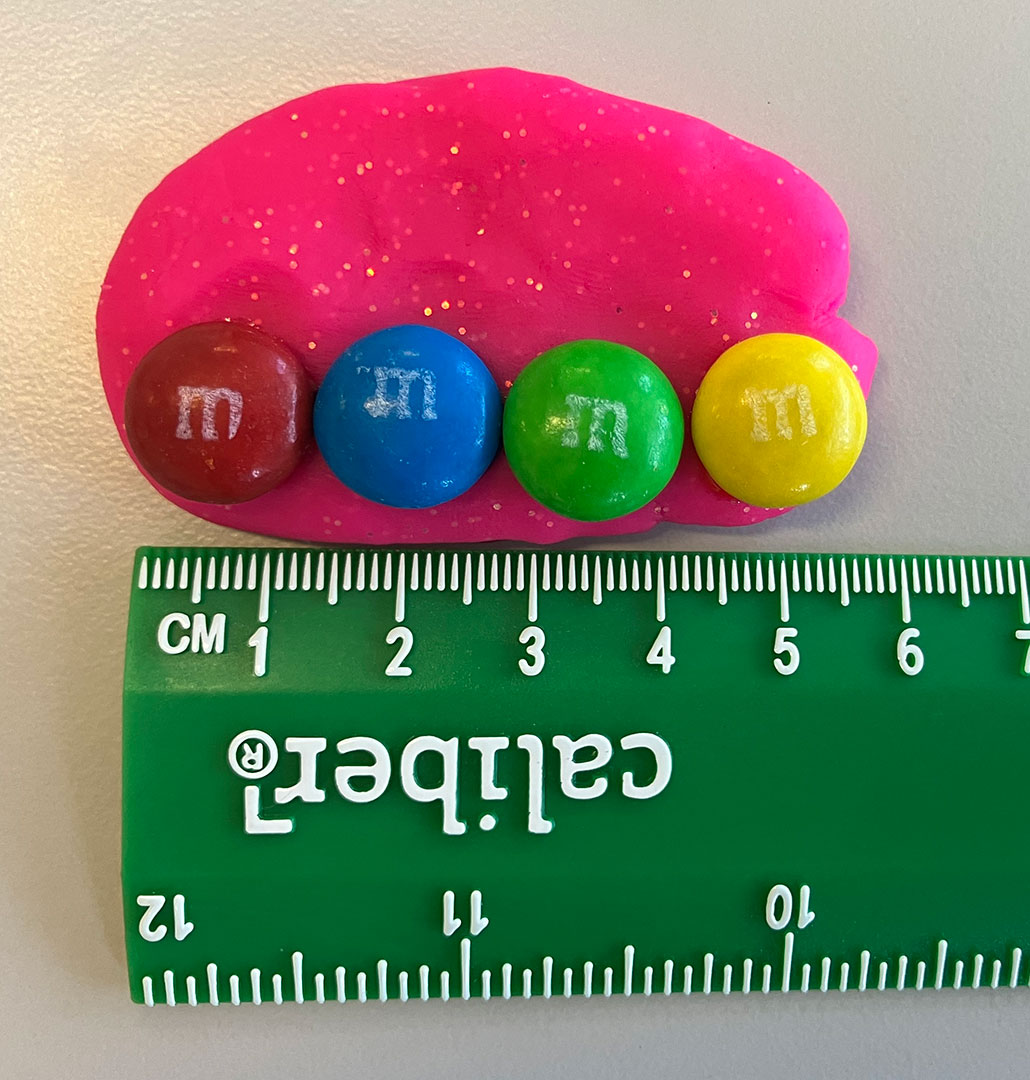
- Measure the whole line of 10 M&M’S from end to end. Write this measurement in the new data table in your lab notebook. Write it in the “Long Side” column as the “Diameter of 10 M&M’S.”
- Divide your answer by 10. This is the long diameter of a single M&M’S candy. Write the data in your data table.
- Divide your answer by 2. This is the long radius of a single M&M’S candy. Write the data in your data table.
- Remove the M&M’S from the clay.
- On the clay, line up the 10 M&M’S on their side so that you are measuring across the short side, or short diameter, as shown in Figure 3.
- Again, use the clay to hold the M&M’S in place in a neat row with each M&M’S touching the next.
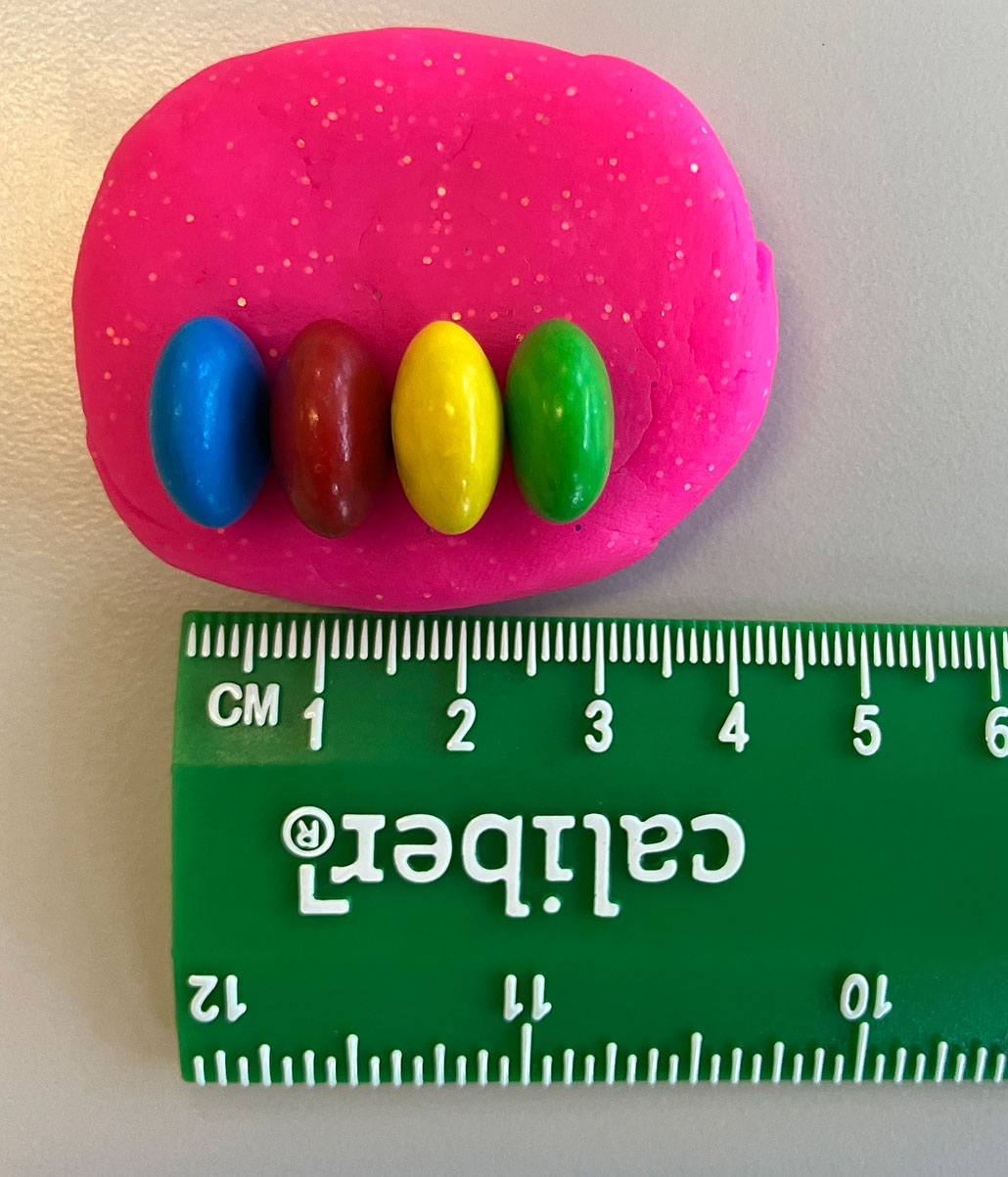
M. Temming
- Repeat steps 5–8, but this time measure and do calculations for the short side of the M&M’S.
- In the data table in your lab notebook, record your measurements in the “Short Side” column.
- Next you will be making some calculations of volume using different formulas to see which one best calculates the volume of the M&M’S. In your lab notebook, make a data table like Table 3 to record your results for each formula.
- For the “Actual Volume” use the value you determined in step 1f. Note: One milliliter is the same as one cubic centimeter (cm3). So, even though you determined the actual volume of one M&M’S candy in milliliters, you can write this value in cubic centimeters instead.
| Calculated volume (cubic cm) | |
| Actual volume | |
| Sphere: long radius | |
| Sphere: short radius | |
| Cylinder | |
| Ellipsoid |
- If you are comfortable doing the math yourself, you can calculate the volumes of different shapes by hand using the formulas on this page. Otherwise you can search for an online volume-calculating tool like http://www.calculator.net/volume-calculator.html, where you can enter the relevant dimensions for each shape and it will calculate the volume for you.
- First you will calculate the volume of a sphere. You will be making the sphere calculation in two ways, with the long radius and the short radius.
- Calculate the volume of a sphere using the long radius. Write the answer in your data table next to “Sphere – Long Radius.”
- Note: Since your measurements are in centimeters, the answers will be in cubic centimeters.
- Calculate the volume of a sphere using the short radius. Write the answer in your data table next to “Sphere – Short Radius.”
- Next you will calculate the volume of a cylinder. Use the M&M’S long radius as the radius of the cylinder and the short diameter (not the short radius) as the height of the cylinder. Write the answer in your data table next to “Cylinder.”
- Next you will calculate the volume of an ellipsoid. Ellipsoids have three axes. Use the M&M’S long radius value for the radius of two of the axes, and the short radius value for the radius of the third axis. Write the answer in your data table next to “Ellipsoid.”
- Now you are ready to make a bar graph of your data. You can make one by hand or you can try using the Create a Graph website for kids from the National Center for Education Statistics.
- Along the x-axis (the horizontal axis), make one bar for each type of volume calculation you did: sphere using the long radius, sphere using the short radius, cylinder and ellipsoid. Also include a bar for the actual volume that you determined in step 1f.
- On the y-axis (the vertical axis), put the volume measurements in cubic centimeters (cm3).
- How do each of the different calculated volumes compare to the actual volume that you measured? Which ones were more and which ones were less? Why do you think this is? Which calculation came the closest? Which formula do you think is the best one to use for an M&M’S candy?
This activity is brought to you in partnership with Science Buddies. Find the original activity on the Science Buddies website.








